算法复杂度计算

定义

算法的时间复杂度使用渐进记号($\Theta$, $O$, $\Omega$, $o$, $\omega$)来描述, 它们的定义如下:

$$ 渐进紧确界: \Theta (g(n))={f(n): 存在常量c_1, c_2和n_0, 使得对所有n>=n_0, 有0<=c_1g(n)<=f(n)<=c_2g(n)} $$
$$ 渐进上界: O(g(n))={f(n): 存在常量c和n_0, 使得对所有n>=n_0, 有0<=cg(n)<=f(n)} $$
$$ 渐进下界: \Omega (g(n))={f(n): 存在常量c和n_0, 使得对所有n>=n_0, 有0<=f(n)<=cg(n)} $$
$$ 非渐进紧确上界: o(g(n))={f(n): 对任意常量c>0, 存在常量n_0>0, 使得对所有n>=n_0, 有0<=f(n)<cg(n)} $$
$$ 非渐进紧确下界: \omega(g(n))={f(n): 对任意常量c>0, 存在常量n_0>0, 使得对所有n>=n_0, 有0<=cg(n)<f(n)}$$

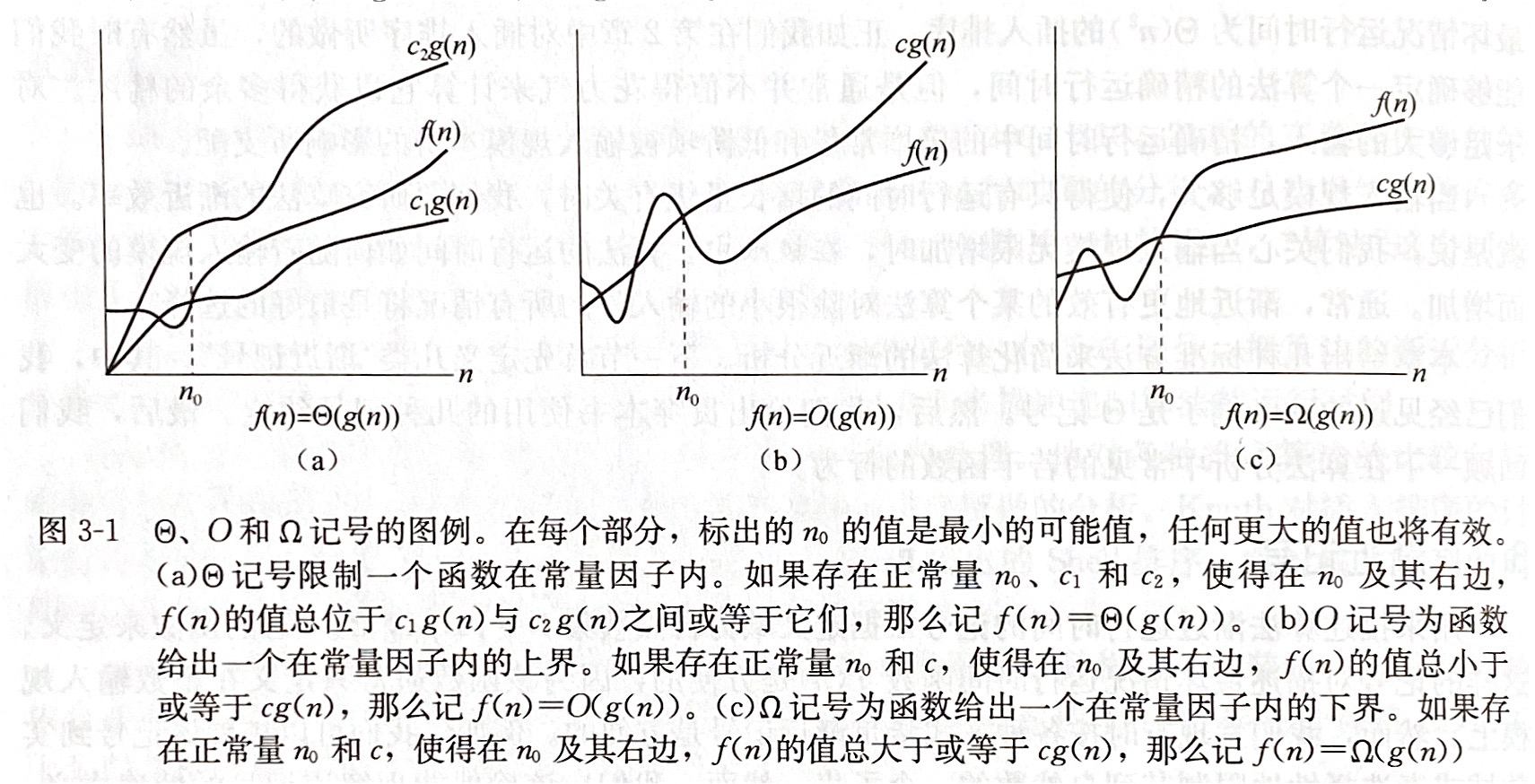
这些渐进记号中平常常用的是前三种($\Theta$, $O$, $\Omega$), 因为日常使用中我们最关心最坏情况下时间复杂度, 所以渐进上界$O$也是最为常用的记号. 对于这三种记号, 结合算法导论上的配图很好理解.

1. $O$描述了最坏情况下的时间复杂度量级;
2. $\Omega$描述了最好情况下的时间复杂度量级;
3. $\Theta$是由$O$和$\Omega$组成的一个区间;

将渐进记号和实数之间的大小比较作类比, 也更好理解:
$$ f(n) = O(n) 类似于 a <= b $$
$$ f(n) = \Omega (n) 类似于 a >= b $$
$$ f(n) = \Theta (n) 类似于 a = b $$
$$ f(n) = o(n) 类似于 a < b $$
$$ f(n) = \omega (n) 类似于 a > b $$

运算

渐进函数具有传递性, 自反性, 对称性和转置对称性. 举例来说:
$$ 传递性: f(n) = O(g(n)) 且 g(n) = O(h(n)) /Rightarrow f(n)=O(h(n)) $$
$$ 自反性: f(n)=O(f(n)) $$
$$ 转置对称性: f(n) = O(g(n)) 当且仅当 g(n) = \Omega (f(n)) $$

利用这些性质可以通过推导的方式得出算法的时间复杂度.

• 以快速排序为例

  1 2 3 4 5 6 7 8

  # 提供一个最好理解的递归实现 def quiksort(l): if len(l) < 2: return l anchor = l[0] left = [i for i in l[1:] if i < anchor] #注意l[1:] right = [i for i in l[1:] if i >= anchor] return quiksort(left) + [anchor] + quiksort(right)

  时间复杂度推导公式如下:
  $$
  \begin{equation}
  \begin{split}
  T(n) &= O(n) + 2 * T(n/2) \
  &= O(n) + 2 * O(n/2) + 4 * T(n/4) \
  &= \sum_{i=1}^{lg(n)} O(n) \
  &= O(nlg(n))
  \end{split}
  \end{equation}
  $$

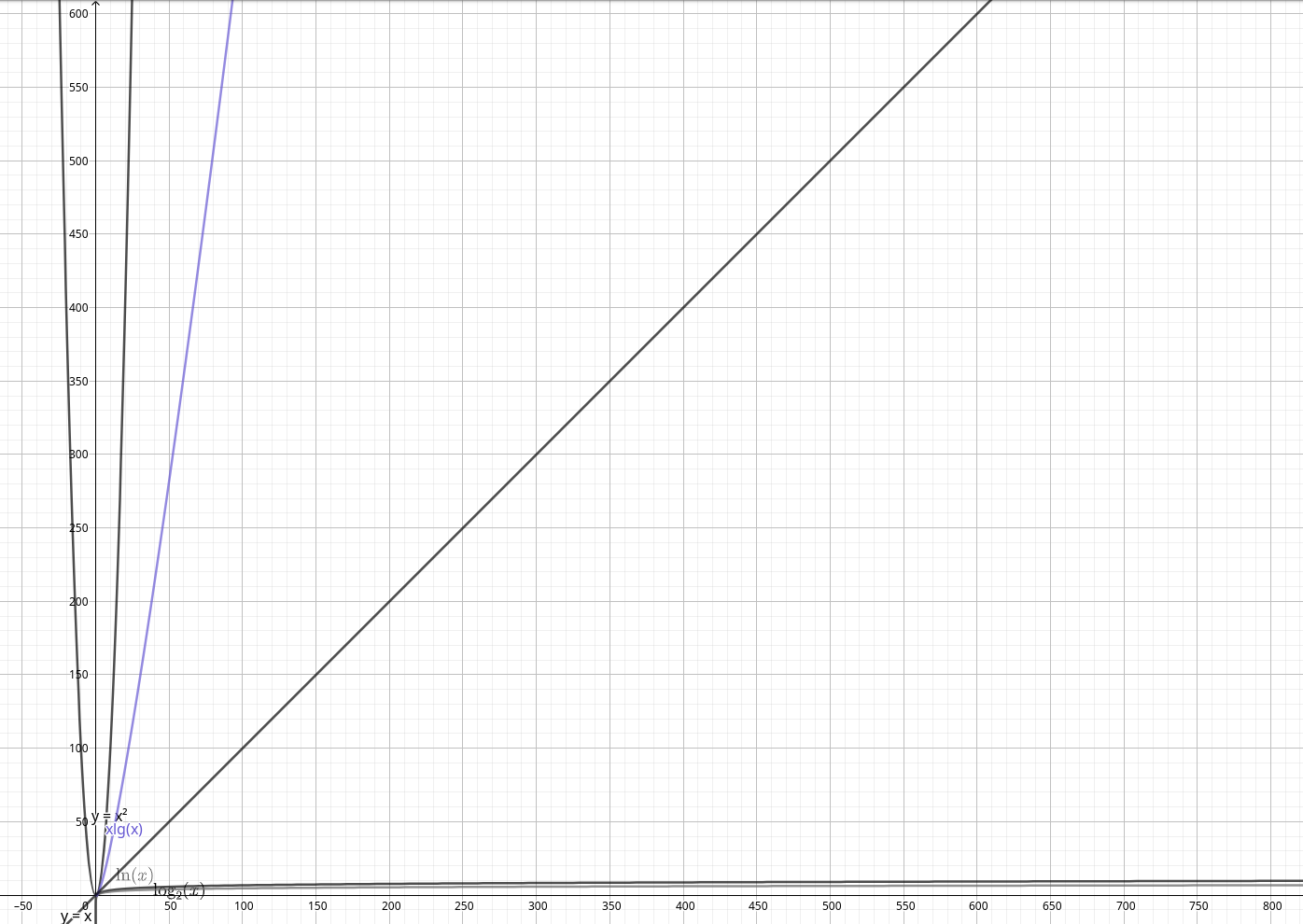
• 附上不同算法复杂度的增长趋势:
  https://www.geogebra.org/calculator/brd6wjte